Metode Numerik

Dalam mencari nilai suatu akar dari suatu persamaan atau permasalahan yang ada, berbagai macam cara dan metode, berikut ini bermacam-macam metode yang dapat kita gunakan dalam mencari nilai suatu akar persamaan :

  1. Metode Bagi Dua (Bisection)
  2. Metode Reguler Falsi
  3. Metode Iterasi Titik Tetap
  4. Metode Newton Rephson
  5. Metode Secant

Dalam kesempatan kali ini saya akan membahas semua metode yaitu metode bagi dua, regular falsi, iterasi titik tetap, newton raphson, secant.


METODE BISECTION

Apa Sih Bisection itu??

    Bisection adalah algoritma pencarian akar pada sebuah interval. Interval tersebut membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan atau mendekati akar persamaan. Metode ini berlaku ketika ingin memecahkan persamaan f(x) = 0 dengan f merupakan fungsi kontinyu.



Rumus 
f(a)*f(b) < 0


Prosedur Metode Bagi-Dua

  • Misal dijamin bahwa f(x) adalah fungsi kontinyu pada interval [a, b] dan f(a)f(b) < 0. Ini artinya bahwa f(x) paling tidak harus memiliki akar pada interval [a, b].
  • Kemudian definisikan titik tengah pada interval [a, b] yaitu c :=. Dari sini kita memperoleh dua subinterval yaitu [a, c] dan [c, b].
  • Setelah itu, cek apakah f(a)f(c) < 0 atau f(b)f(c) < 0 ?
    • Jika f(a)f(c) < 0 maka b = c (artinya titik b digantikan oleh titik c yang berfungsi sebagai titik b pada iterasi berikutnya),
    • jika tidak maka a = c. Dari iterasi pertama kita memperoleh interval [a, b] yang baru dan titik tengah c yang baru.
  • Kemudian lakukan pengecekan lagi seperti sebelumnya sampai memperoleh error yang cukup kecil.


Contoh Soal !!

kerjakan akar dari 𝑓(𝑥) = 𝑥^3 − 𝑥 ^ − 𝑥 + 1 = 0 menggunakan metode biseksi dan dengan program yang kalian ketahui!

source code 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<stdio>
#include<math.h>
 
float f(float x){
    return (pow(x,3.0))-(pow(x,2.0))-x+1;
}
 
void RegulaFalsi(float atas, float bawah, int iterasi){
     
    int i=0;
    float c;
    float fb,fc,fa;
    printf("RegulaFalsi\n");
    while(i<iterasi){
        fb=f(bawah);
        fa=f(atas);
        c= bawah - (fb/(fb-fa)) * (bawah-atas);
         
        fc=f(c);
        printf("Iterasi %d:\t Xr %f\t F(Xr)\t%f\n",i+1,c,fc);
         
        if(fb*fc<0){
            atas=c;
        }else{
            bawah=c;
        }
        i++;
    }
     
} 
void BisectionMethod(float atas, float bawah, int iterasi)
{
    float fb,fc,fa;
    float c;
    int n;
    printf("Bisection\n");
    for (n = 0; n < iterasi; n++)
    {
         
        fb=f(bawah);
        fa=f(atas);
         
        c = (bawah + atas) / 2;
        c = roundf(c * 1000) / 1000;
        fc=f(c);
        
       printf("Iterasi %d:\t Xr %f\t F(Xr)\t%f\n",n+1,c,fc); 
       if (fc * fb < 0)
       {
         atas = c;
       }
       else
       {
         bawah = c;
       }     
       }
     
}
 
int main(){
    float a,b,c;
    int iterasi;
    a=1;
    b=3;
    c=0;
     
    printf("(pow(x,3.0))-(pow(x,2.0))-x+1\n");
    printf("masukan iterasi\n");
    scanf("%d",&iterasi);
     
    RegulaFalsi(a, b, iterasi);
    BisectionMethod(a, b, iterasi);
     
}


output



Pembuktian



METODE REGULA FALSI

    Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dari dua titik batas range. Sebenarnya metode ini hampir sama dengan Metode Biseksi, tapi titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi. 


Rumus 


Contoh Soal !!

kerjakan akar dari 𝑓(𝑥) = 𝑥 3 − 𝑥 2 − 𝑥 + 1 = 0 menggunakan metode biseksi dan regula falsi dan dengan program yang kalian ketahui!

source code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<stdio.h>
#include<math.h>
double f(double x)
{
	return(pow(x,3.0))-(pow(x,2.0))-x+1;
}
main()
{
	double y[100],a,b,e,y1,y2,xr,y3;
	int n,i=0;
	printf("\t\tMetode Regula falsi\t\t\n");
	
	printf("masukkan batas bawah=");
	scanf("%lf",&a);
	printf("masukkan batas atas=");
	scanf("%lf",&b);
	printf("masukkan toleransi error=");
	scanf("%lf",&e);
	printf("masukkan iterasi maksimum=");
	scanf("%d",&n);
	y1=f(a);
	y2=f(b);
	
	if(y1*y2>0)
		printf("tidak ditemukan akar\n");
	else
	{ 
		i<=n;
	
	printf("a |\tb |\t\txr|\tf(a) |\t\tf(b) |\tf(x) \n");
	printf("==================================================================\n");
			while (i<=n)
			{
			xr=((y2*a)-(y1*b))/(y2-y1);
			y[i]=f(xr);
			y3=f(xr);
			printf("|%3d|%.7lf|%.7lf|%.7lf|%.7lf|%.7lf|\n",i+1, a, b, xr, y1,f(xr));
			if(y[i]*y1<0)
			{	b=xr;
				y2 = f(xr);
			}
			else
			{	a=xr;
				y1 = f(xr);
			}
			i++;
			if(fabs(b-a)<=e || i>(n-1))
				break;
		}
		
		printf("=====================================================================\n");
		printf("Akar persamaan adalah %lf\n",xr);
		if (f(xr)<0)
		{
			y3=(fabs(y2*-1));

			printf("Nilai error = %.7f\n",y3);
		}
		else
			printf("Nilai error = %.7f\n",y3);
	}
}

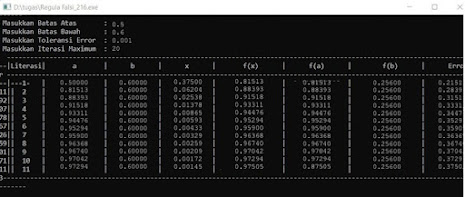
output


Pembuktian



METODE ITERASI TITIK TETAP

Metode iterasi titik tetap disebut juga metode  iterasi  sederhana, metodelangsung,   atau   metode  substitusi  beruntun.  Metode   iterasi   titik   tetap   adalahmetode yg memisahkan x dengan sebagian x yang lain sehingga diperoleh: x =g(x).

Prosedur 

Kesederhanaan metode ini karena pembentukan prosedur iterasinya  yang mudah dibentuk sebagai berikut.

  1. Ubah persamaan f(x)=0 menjadi bentuk x=g(x)
  2. Bentuk menjadi prosedur iterasi xr+1=g(x¿¿r)¿
  3. Terka sebuah nilai awal x0
  4. Hitung   nilai  x1,x2,x3,...,  yang  konvergen ke suatu titik s

Contoh Soal !!

Carilah akar persamaan 𝑓(𝑥) = 𝑥^3 − 𝑥^2 − 𝑥 + 1 = 0 dengan metode iterasi titik tetap dan menggunakan program yang kalian ketahui!

      Pembahasan
  • Terdapat beberapa kemungkinan prosedur iterasi yang dapat dibentuk
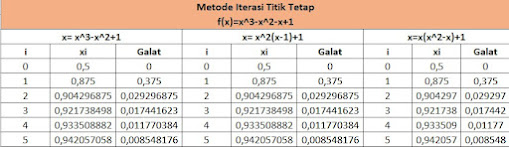
    1. x = x^3 - x^2 +1
    2. x = x^2 (x-1) +1
    3. x = x (x^2-x) +1
source code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <stdio.h>
#include <iostream>
#include <conio.h>
#include <math.h>
using namespace std;
float eth,x[20];
int i=-1;
float F(float x){
    return (pow(x,3.0))-(pow(x,2.0))-x+1;
}
float G(float x){
    return ((pow(x,2.0))*(x-1))+1;
}
main ()
{
   
    cout << " Metode Iterasi Sederhana\n"<<endl;
    cout << " Masukkan Nilai Awal : ";
    cin >> x[0];
    cout << "\n Masukkan Batas Toleransi : ";
    cin >> eth;           

            printf(" \n iterasi\t  x(i)\t\t akar\t\t fx(i+1)\n");
            do
            {
                i++;
                x[i+1]= G(x[i]);
                printf("\n   %d\t %f\t %f\t %f\t\n",i+1,x[i],x[i+1],F(x[i+1]));
            }
            while (fabs(F(x[i+1])) > eth);
            printf("\n akar = %f \n",x[i+1]);
getch();       
}


output

x = x^3 - x^2 +1
 

x = x^2 (x-1) +1

x = x (x^2-x) +1


Pembuktian 



METODE NEWTON REPSHON

    Metode Newton Raphson diperkenalkan oleh Sir Isaac Newton (1643-1727) dan Joseph Raphson (1648–1715) yang dipergunakan untuk pencarian akar real dari persamaan non linear. Metode Newton Raphson ini memiliki keuntungan dibandingkan metode yang lain seperti Bisection atau Secant karena hanya membutuhkan satu nilai aproksimasi dan jumlah iterasi (konvergensi) yang lebih sedikit terutama jika nilai aproksimasi awal yang dipilih berada "dekat" dengan akar yang akan dicari.



Keterangan:

Garis singgung yang melalui (x0, f(x0)) akan memotong sumbu x di x1. Nilai x1 inilah yang menjadi aproksimasi berikutnya. Nilai x1 kita peroleh menggunakan formula:


Prosedur Newton Repshon

Algoritma metode Newton Raphson dengan metode geometri adalah sebagai berikut:

  1. Mulai
  2. Tentukan nilai aproksimasi awal x0
  3. Cari nilai fx0 dan f'x0
  4. Cari nilai x1 = x0 - (fx0/f'x0)
  5. Cari nilai error  = |x1-x0|
  6. x0 = x1
  7. Jika nilai error > toleransi error maka ulangi langkah 2, jika tidak tampilan x0 sebagai akar persamaan yang dicari
  8. Selesai

Contoh Soal

𝑓(𝑥) = 𝑥 3 − 𝑥 2 − 𝑥 + 1 = 0 dengan metode newton-raphson dan menggunakan program yang kalian ketahui!

source code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>
#include <iostream>
#include <conio.h>
#include <math.h>
using namespace std;
float eth,x[20];
int i=-1;
float F(float x){
    return (pow(x,3.0))-(pow(x,2.0))-x+1 ;
}
float Ft(float x){
    return (3.0*pow(x,2.0))-(2.0*x)+1;
}
main ()
{
   
    cout << " Metode Newton Raphson\n"<<endl;
    cout << " Masukkan Nilai Awal : ";
    cin >> x[0];
    cout << "\nMasukkan Batas Toleransi : ";
    cin >> eth;           

            printf("\niterasi\t  x(i)\t\t x(i+1)\t\t fx(i+1)\t f'x(i+1)\n");

            do

            {
                i++;
                x[i+1]= ((x[i]) - ( F(x[i]) / Ft(x[i])));
                printf("\n%d\t %f\t %f\t %f\t %f\t\n",i+1,x[i],x[i+1],F(x[i+1]),Ft(x[i+1]));
            }
            while (fabs(F(x[i+1])) > eth);
            printf("\nakar = %f \n",x[i+1]);
getch();       
}

output

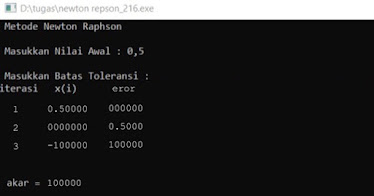
Pembuktian



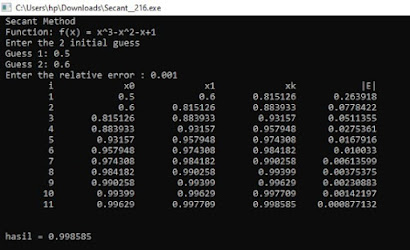
METODE SECANT

Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik. Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f‘(x).


Prosedur Metode Secant
  1. Definisikan fungsi F(x)
  2. Definisikan torelansi error (e) dan iterasi maksimum (n)
  3. Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya  gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.
  4. Hitung F(x0) dan F(x1) sebagai y0 dan y1
  5. Untuk iterasi I = 1 s/d n atau | F(xn) | Xn+1 = Xn – Yn (Xn – Xn-1 / Yn – Yn-1) 

Rumus 

Contoh Soal !!

𝑓(𝑥) = 𝑥 3 − 𝑥 2 − 𝑥 + 1 = 0 dengan metode secant dan menggunakan program yang kalian ketahui!

source code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <conio.h>
#include <cmath>
#include <iomanip>
using namespace std;
float f(float x);
int main() {
float d,e,r,q,p,n,epsilon;
float s;
cout<<" Secant Method "<<endl;
cout<<"Function: f(x) = (x1*x1*x1)-(x1*x1)-(1)+ 1 "<<endl;
cout<<"Enter the 2 initial guess "<<endl;
cout<<"Guess 1: ";cin>>d;
cout<<"Guess 2: ";cin>>e;
cout<<"Enter the relative error [E]: "; cin>>epsilon;
n=1;
if(e>d)
    {p=d;
    q=e;}
else
    {q=d;
    p=e;}
cout<<setw(10)<<"i"<<setw(15)<<"x0"<<setw(15)<<"x1";
cout<<setw(15)<<"xk"<<setw(15)<<"|E|"<<endl;
do{
    r=q-((f(q)*(q-p))/(f(q)-f(p)));
    s=fabs((r-q)/r);
    cout<<setw(10)<<n<<setw(15)<<p<<setw(15)<<q<<setw(15)<<r<<setw(15)<<s<<endl;
    p=q;
    q=r;
    n++;
} while (n<30 && s>epsilon && s!=0);
cout<<"\n\n hasil = "<<r;
cout<<endl<<endl<<endl;

return 0;
}
float f( float x) {
    return (pow(x,3.0))-(pow(x,2.0))-(x)+(1);
}


output



Pembuktian



Semoga rangkuman "Metode Numerik" ini bermanfaat dan apabila ada salah  kata di dalam blog yang saya tulis, saya minta maaf. 

Jika ingin mengenal lebih dalam tentang Universitas saya, silahkan akses link berikut: umsida.ac.id, fst.umsida.ac.id  

Sekian dan Terima Kasih.


saniya izza fitria_216



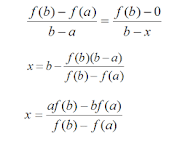
Tidak ada komentar:

Posting Komentar

Langganan: Postingan (Atom)